حقیقت چیه؟ ارسطو فکر میکرد منطق یه جور ربطی به حقیقت داره. مجموعهای از آموزههاش به اسم «ارگانون» که به قرن چهارم پیش از میلاد برمیگرده، قدیمیترین نوشتههای مفصل درباره منطق حساب میشه. برای یونانیهای قدیمی، منطق راهی بود برای تحلیل زبان به دنبال حقیقت، و به همین خاطر منطق رو نوعی فلسفه میدونستن. پایه منطق ارسطو هم قیاس بود. معروفترین قیاس (که البته توی آثار ارسطو نیست) اینه:
همهی آدمها فانی هستن؛
سقراط آدمه؛
پس سقراط فانیه.
تو یه قیاس، دو فرض درست در نظر گرفته میشه و از اونها یه نتیجه گرفته میشه.
فانی بودن سقراط شاید ساده به نظر بیاد، اما قیاسهای مختلفی وجود داره. مثلاً این دو فرضی که ریاضیدان قرن نوزدهم، چارلز داجسون (یا همون لوئیس کارول) گفته:
همه فیلسوفها منطقیان؛
آدم غیرمنطقی همیشه لجبازه.
نتیجه اینکه «بعضی از آدمهای لجباز فیلسوف نیستن» اصلاً واضح نیست. به کلمهی «بعضی» دقت کن که ناگهانی و کمی عجیب به نظر میرسه.
بیش از دو هزار سال، ریاضیدانها با منطق ارسطو دست و پنجه نرم کردن و سعی کردن با نمادها و علامتهای ریاضی اون رو محدود کنن. تا قبل از قرن نوزدهم، تنها کسی که تا حدی موفق شده بود گوتفرید ویلهلم فون لایبنیتس بود که اول زندگی کمی سر و کار با منطق داشت، اما بعد به سراغ چیزهای دیگه رفت، مثل اینکه همزمان با نیوتن، حساب دیفرانسیل و انتگرال رو کشف کرد.
بعدش جورج بول اومد.
جورج بول در سال ۱۸۱۵ توی انگلستان به دنیا اومد، تو شرایطی که واقعاً همه چیز به ضررش بود. چون پسر یه کفاش و یه خدمتکار سابق بود، ساختار سخت طبقهبندی اجتماعی بریتانیا معمولاً اجازه نمیداد از پیشینیانش جلوتر بره. اما با ذهن کنجکاوش و کمکهای پدرش که به علوم، ریاضی و ادبیات علاقه داشت، جورج تونست تحصیلاتی داشته باشه که معمولاً مخصوص پسرهای طبقه بالا بود؛ درسهای لاتین، یونانی و ریاضی رو یاد گرفت. به خاطر مقالات اولیهاش تو ریاضی، سال ۱۸۴۹ به عنوان اولین استاد ریاضی تو کالج کوئینز کورک ایرلند انتخاب شد.

چندتا ریاضیدان در اواسط قرن نوزدهم، از جمله آگوستوس دِ مورگان، روی تعریف ریاضی منطق کار میکردن، اما این جورج بول بود که واقعا یک جهش مفهومی بزرگ داشت. اول تو کتاب کوتاهش با عنوان «تحلیل ریاضی منطق، که تلاشی برای حساب استنتاج است» (۱۸۴۷)، و بعد تو یک کتاب بلندتر و بلندپروازانهتر به اسم «تحقیق در قوانین تفکر که پایههای نظریههای ریاضی منطق و احتمالاند» (۱۸۵۴) که بهصورت خلاصه بهش «قوانین تفکر» میگفتن. بول در سال ۱۸۶۴ وقتی ۴۹ ساله بود، بعد از اینکه تو بارون سریع رفت سر کلاس و دچار ذاتالریه شد، فوت کرد.
عنوان کتاب ۱۸۵۴ بول نشون میده انگیزهی بلندپروازانهای داشته: بول معتقد بود که مغز انسان برای فکر کردن از منطق استفاده میکنه، پس اگر بتونیم منطق رو با ریاضیات نمایش بدیم، درواقع یه توصیف ریاضی از کارکرد مغز خواهیم داشت. ولی ریاضیات بول رو میشه بدون قبول کردن کامل اون دیدگاه روانشناسی عصبیاش هم مطالعه کرد.
بول نوعی جبر کاملاً متفاوت اختراع کرد که بعدها به افتخار اون «جبر بولی» نامیده شد تا از جبر معمولی متمایز بشه.
تو جبر معمولی، معمولاً از حروف برای نمایش اعداد استفاده میکنیم. اینها رو عملوند میگن و با عملگرها (مثل + و ×) به روشهای مختلف ترکیب میکنن. مثلاً:
A = ۳ × (B + ۵)
وقتی جبر معمولی انجام میدیم، قوانین خاصی رو دنبال میکنیم. این قوانین آنقدر تو کارمون جا افتادن که دیگه شاید بهشون فکر نکنیم و حتی اسمشون یادمون بره، اما همه ریاضیات بر پایه همین قوانین بنا شده.
اولین قانون اینه که جمع و ضرب جابهجاپذیر هستن. یعنی میتونیم جای عملوندها رو عوض کنیم:
A + B = B + A
A × B = B × A
برعکسش، تفریق و تقسیم جابهجاپذیر نیستن.
جمع و ضرب همچنین انجمایی هستن، یعنی:
A + (B + C) = (A + B) + C
A × (B × C) = (A × B) × C
و در نهایت، ضرب توزیعپذیر نسبت به جمعه:
A × (B + C) = (A × B) + (A × C)
یکی دیگه از ویژگیهای جبر معمولی اینه که همیشه با عدد کار میکنه، مثل وزن توفو، تعداد اردکها، مسافتی که یه قطار طی میکنه یا ثانیههای یک روز.
نوآوری بزرگ بول این بود که جبر رو از مفهوم عدد جدا کرد و به شکلی انتزاعیتر تبدیلش کرد. تو جبر بولی، عملوندها به جای عدد، به دستهها اشاره دارن. یه دسته یعنی گروهی از چیزها، چیزی شبیه به چیزی که بعدها بهش مجموعه (ست) گفته شد.
بیا درباره گربهها حرف بزنیم. گربهها یا نر هستن یا ماده. برای راحتی کار میتونیم از حرف M برای کلاس گربههای نر و از F برای کلاس گربههای ماده استفاده کنیم. یادت باشه این دو حرف نمایانگر تعداد گربهها نیستن. تعداد گربههای نر و ماده ممکنه هر لحظه تغییر کنه چون گربههای جدید به دنیا میان و گربههای قدیمی (متأسفانه) میرن. این حروف فقط نشوندهنده دستهای از گربهها با ویژگیهای خاص هستن. به جای گفتن «گربههای نر»، میتونیم فقط بگیم «M».
همچنین میتونیم از حروف دیگهای برای رنگ گربهها استفاده کنیم. مثلاً T برای کلاس گربههای قهوهای روشن، B برای کلاس گربههای سیاه، W برای گربههای سفید، و O برای گربههای بقیه رنگها—همه گربههایی که تو کلاس T، B یا W نیستن.
در نهایت (حداقل برای این مثال)، گربهها یا عقیم شدن یا عقیم نشدن. برای کلاس گربههای عقیم شده از N و برای کلاس گربههای عقیم نشده از U استفاده میکنیم.
تو جبر معمولی (عددی)، عملگرهای + و × برای جمع و ضرب به کار میرن. تو جبر بولی هم همین + و × استفاده میشن و اینجا ممکنه قضیه گیجکننده بشه. همه میدونن چطور اعداد رو جمع و ضرب کنن، اما چطور کلاسها رو جمع و ضرب کنیم؟
راستش تو جبر بولی ما واقعاً جمع و ضرب انجام نمیدیم. به جای اون، نمادهای + و × معنی کاملاً متفاوتی دارن.
علامت + تو جبر بولی یعنی اجتماع دو کلاس. اجتماع دو کلاس یعنی همه چیزهایی که تو کلاس اول هستن به اضافه همه چیزهایی که تو کلاس دوم هستن. مثلاً B + W یعنی کلاس همه گربههایی که یا سیاه هستن یا سفید.
علامت × تو جبر بولی یعنی اشتراک دو کلاس. اشتراک دو کلاس یعنی همه چیزهایی که هم تو کلاس اول هستن و هم تو کلاس دوم. مثلاً F × T یعنی کلاس همه گربههایی که هم ماده هستن و هم قهوهای روشن. مثل جبر معمولی، میتونیم F × T رو به صورت F·T یا فقط FT هم بنویسیم (که بول خودش بیشتر همین رو ترجیح میداد). میتونیم این دو حرف رو مثل دو صفت پشت هم تصور کنیم: «گربه ماده قهوهای».
برای اینکه بین جبر معمولی و بولی اشتباهی پیش نیاد، گاهی به جای + و × از نمادهای ∪ و ∩ برای اجتماع و اشتراک استفاده میکنن. ولی یکی از کارهای آزادکننده بول تو ریاضیات این بود که از عملگرهای آشنا استفاده کنه و نشانههای جدید معرفی نکنه، پس من هم تصمیم گرفتم مثل بول عمل کنم و نشانههای جدید وارد نکنم.
قوانین جابهجایی، انجماعی و توزیعی همگی تو جبر بولی برقرارن. علاوه بر این، تو جبر بولی عملگر + روی × توزیعپذیره که تو جبر معمولی اینطوری نیست:
W + (B × F) = (W + B) × (W + F)
یعنی اجتماع گربههای سفید و گربههای ماده سیاه برابر با اشتراک دو اجتماع هست: اجتماع گربههای سفید و سیاه، و اجتماع گربههای سفید و ماده. این موضوع شاید کمی سخت باشه اما درسته.
سه نماد دیگه لازمه تا جبر بولی کامل بشه. دو تا از این نمادها ممکنه شبیه عدد باشن، اما واقعاً نیستن چون کمی متفاوت از اعداد رفتار میشن. نماد ۱ تو جبر بولی یعنی «جهان» — یعنی همه چیزهایی که داریم دربارهش حرف میزنیم. تو این مثال، نماد ۱ یعنی «کلاس همه گربهها». بنابراین:
M + F = 1
یعنی اجتماع گربههای نر و ماده میشه کلاس همه گربهها. به همین ترتیب، اجتماع گربههای قهوهای، سیاه، سفید و بقیه رنگها هم میشه کلاس همه گربهها:
T + B + W + O = 1
و همچنین میتونیم کلاس همه گربهها رو اینطوری به دست بیاریم:
N + U = 1
نماد ۱ رو میتونیم همراه با علامت منفی استفاده کنیم تا جهان رو به جز یه چیز خاص نشون بدیم. مثلاً:
۱ − M
یعنی کلاس همه گربهها به جز گربههای نر. جهان بدون همه گربههای نر، همون کلاس گربههای ماده است:
۱ − M = Fنماد سومی که لازمش داریم، ۰ (صفر) هست که تو جبر بولی یعنی کلاس خالی — یعنی کلاسی که هیچ عضوی نداره. کلاس خالی وقتی به دست میاد که اشتراک دو کلاس که کاملاً متضاد هم هستن رو بگیریم؛ مثلاً گربههایی که هم نر هستن و هم ماده:
F × M = 0
توجه کن که نمادهای ۱ و ۰ گاهی تو جبر بولی مثل جبر معمولی عمل میکنن. مثلاً:
اشتراک همه گربهها و گربههای ماده میشه کلاس گربههای ماده:
۱ × F = F
اشتراک هیچ گربهای با گربههای ماده میشه کلاس هیچ گربهای:
۰ × F = ۰
اجتماع هیچ گربهای با همه گربههای ماده میشه کلاس گربههای ماده:
۰ + F = F
اما گاهی نتیجه مثل جبر معمولی نیست. مثلاً اجتماع همه گربهها و گربههای ماده میشه کلاس همه گربهها:
۱ + F = ۱
که تو جبر معمولی معنی خاصی نداره.
چون F یعنی کلاس همه گربههای ماده، و (۱ − F) یعنی کلاس همه گربههایی که ماده نیستن، اجتماع این دو کلاس میشه ۱:
F + (۱ − F) = ۱
و اشتراک این دو کلاس میشه ۰:
F × (۱ − F) = ۰
این قانون تاریخی، یه مفهوم مهم تو منطق رو نشون میده: قانون تضاد، یعنی یه چیز نمیتونه هم خودش باشه و هم عکس خودش.
اونجا که جبر بولی واقعاً فرق میکنه با جبر معمولی، جملههایی مثل اینه:
F × F = F
که کاملاً منطقیه تو جبر بولی: اشتراک گربههای ماده با خودشون میشه باز هم کلاس گربههای ماده. ولی اگه F عدد بود، این جمله درست به نظر نمیرسید.
بول این رو مهمترین تفاوت جبر خودش با جبر معمولی میدونست و این رو به صورت:
X² = X
بیان میکرد.
یه جمله دیگه که تو جبر معمولی عجیب به نظر میاد اینه:
F + F = F
یعنی اجتماع گربههای ماده با خودشون باز هم کلاس گربههای ماده است.
جبر بولی روش ریاضیای برای حل سلیقههای ارسطو ارائه میده. بیاید دوباره دو بند اول همون سلیقه معروف رو با زبان بیطرف جنسیتی مرور کنیم:
همه افراد فانی هستن؛
سقراط یک فرد است.
ما از P برای کلاس همه افراد، M برای کلاس همه موجودات فانی، و S برای کلاس سقراط استفاده میکنیم. وقتی میگیم «همه افراد فانی هستن» یعنی اشتراک کلاس همه افراد و کلاس همه موجودات فانی، میشه کلاس همه افراد:
P × M = P
نمیشه گفت P × M = M چون کلاس همه موجودات فانی شامل گربهها، سگها و درختان هم هست.
وقتی میگیم «سقراط یک فرده»، یعنی اشتراک کلاس سقراط (که یه کلاس خیلی کوچیکه) با کلاس همهی افراد (که بزرگتره) میشه همون کلاس سقراط:
S × P = S
حالا چون از معادلهی اول میدونیم که P برابر با (P × M) هست، میتونیم اینو جایگزین کنیم توی معادله دوم:
S × (P × M) = S
طبق قانون شرکتپذیری، این برابر با اینه که:
(S × P) × M = S
ولی ما از قبل میدونیم که (S × P) برابر با S هست، پس میتونیم سادهترش کنیم:
S × M = S
و حالا کار تمومه. این فرمول میگه اشتراک سقراط و کلاس موجودات فانی، خود سقراطه، یعنی «سقراط فانیه».
اگه در عوض، میدیدیم که (S × M) برابر با ۰ هست، اونوقت نتیجه میگرفتیم که «سقراط فانی نیست».
اگه (S × M) برابر با M میشد، یعنی همهی موجودات فانی فقط خود سقراط بودن!
ممکنه استفاده از جبر بولی برای اثبات چنین نکتهی واضحی یه جور «زیادهروی» به نظر برسه (بهخصوص وقتی بدونیم سقراط خودش ۲۴۰۰ سال پیش فانی بودنش رو نشون داد!)، ولی جبر بولی میتونه برای بررسی اینکه آیا چیزی با یهسری شرایط خاص تطابق داره یا نه، خیلی به کار بیاد.
مثلاً یه روز وارد یه پتشاپ میشی و به فروشنده میگی:
«من یه گربهی نر میخوام، اختهشده، یا سفید باشه یا کرم؛ یا یه گربهی ماده، اختهشده، به هر رنگی غیر از سفید؛ یا هر گربهای که سیاه باشه هم قبوله.»
و فروشنده میگه:
«پس شما دنبال گربهای هستی که تو این کلاس قرار میگیره:
(M × N × (W + T)) + (F × N × (1 − W)) + B
درسته؟»
و تو میگی: «دقیقاً! همینه!»
برای اینکه مطمئن بشی حرف فروشنده درسته، شاید بخوای از کلمات یا (OR) و و (AND) برای نشوندادن اجتماع و اشتراک استفاده کنی.
من این کلمات رو با حروف بزرگ مینویسم چون علاوه بر معنای معمولشون تو زبان انگلیسی، توی جبر بولی هم معنی خاصی دارن.
وقتی اجتماع دو کلاس رو میگیریم، یعنی از کلاس اول یا کلاس دوم عضو میپذیریم.
وقتی اشتراک دو کلاس رو میگیریم، فقط اونهایی رو قبول میکنیم که تو هردو کلاس باشن.
و وقتی چیزی رو میخوایم نباشه، از واژهی نه (NOT) استفاده میکنیم که همون 1 منهای اون چیزه.
خلاصه اینکه:
- O یعنی OR (یا)
- × یعنی AND (و)
- 1 − یعنی NOT (نه)
پس اون عبارت رو میتونیم اینطوری هم بنویسیم:
(M AND N AND (W OR T)) OR (F AND N AND (NOT W)) OR B
این دقیقاً همون چیزیه که گفتی. ببین چطوری پرانتزها نیتت رو دقیقتر نشون میدن. تو دنبال گربهای از یکی از این سه دسته هستی:
- نر، اختهشده، سفید یا کرم
- ماده، اختهشده، غیرسفید
- یا فقط سیاه
وقتی این فرمول رو بنویسی، فروشنده میتونه از چیزی به اسم آزمون بولی (Boolean Test) استفاده کنه. این شامل یه نوع دیگه از جبر بولیه، جایی که حروف بیانگر ویژگیهای خاص هستن، و بهشون مقدار ۱ یا ۰ داده میشه.
عددی که ۱ باشه یعنی بله، درسته، این گربه اون ویژگی رو داره؛
عددی که ۰ باشه یعنی نه، این ویژگی رو نداره.
اولین گربهای که فروشنده میاره، یه نرِ اختهنشدهی کرمرنگه.
فرمولی که مشخص میکنه چه گربههایی مورد قبوله، اینه:
(M×N×(W+T))+(F×N×(1−W))+B
و حالا این فرمول، وقتی ۰ و ۱ بهجای ویژگیهای گربه جایگزین بشن، به این شکل در میاد:
(1×0×(0+1))+(0×0×(1−0))+0
دقت کن که تنها نمادهایی که مقدارشون ۱ هست، M و T هستن، چون گربه نره و رنگش کرمه.
حالا کاری که باید بکنیم اینه که این عبارت رو ساده کنیم.
اگه در نهایت بشه ۱، یعنی این گربه با معیارهای تو جور درمیاد.
اگه بشه ۰، یعنی نه، بهدردت نمیخوره.
موقع ساده کردن این عبارت، باید در نظر داشته باشیم که ما واقعاً داریم جمع و ضرب عددی انجام نمیدیم، هرچند در بیشتر مواقع میتونیم طوری وانمود کنیم که داریم انجامشون میدیم.
بیشتر قوانین معمول جمع و ضرب، وقتی که + بهمعنی OR و × بهمعنی AND باشه، همچنان برقرارن. (تو بعضی متنهای جدیدتر، بهجای × و + از نمادهای ∧ و ∨ برای AND و OR استفاده میکنن. اما علامتهای + و × ممکنه کار رو آسونتر کنن، چون شبیه همونهاییان که تو جبر معمول استفاده میشن.)
وقتی علامت × بهمعنی AND باشه، حالتهای ممکن اینطوریان:
0×0 = 0
0×1 = 0
1×0 = 0
1×1 = 1
یعنی فقط وقتی نتیجه میشه ۱ که هم عامل سمت چپ، هم عامل سمت راست ۱ باشن.
این عملیات دقیقاً مثل ضرب معمولی عمل میکنه و میشه خلاصهش رو توی یه جدول دید:
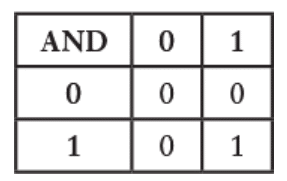
وقتی علامت + بهمعنی OR باشه، حالتهای ممکنش اینطوریان:
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 1
نتیجه فقط وقتی میشه ۱ که یا عامل سمت چپ، یا عامل سمت راست، یا هر دو برابر با ۱ باشن.
این عملیات از نظر نتیجه خیلی شبیه جمع معمولیه، فقط با این تفاوت که توی اینجا ۱ + ۱ همچنان ۱ میشه.
(مثلاً اگه یه گربه کرمرنگ باشه یا کرمرنگ باشه، خب مشخصه که کرمرنگه!)
عملیات OR رو میتونیم با یه جدول کوچیک خلاصه کنیم:
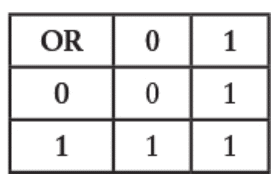
الان آمادهایم که از این جدولها استفاده کنیم و عبارت زیر رو حساب کنیم:
(1×0×1)+(0×0×1)+0 = 0+0+0 = 0
نتیجه: ۰، یعنی نه، جواب منفیه—این گربه نمیخوره به چیزی که دنبالش بودی.
بعد، فروشنده یه گربهی مادهی سفید و عقیمشده میاره. فرمول اولیه این بود:
(M × N × (W + T)) + (F × N × (1 − W)) + B
حالا جای نمادها رو با صفر و یک عوض میکنیم:
(0 × 1 × (1 + 0)) + (1 × 1 × (1 − 1)) + 0
و سادهسازی میکنیم:
(0 × 1 × 1) + (1 × 1 × 0) + 0 = 0 + 0 + 0 = 0
یعنی این یکی گربهی بیچاره هم باید رد بشه.
حالا فروشنده یه گربهی مادهی خاکستری و عقیمشده میاره. (رنگ خاکستری جزو دستهی «سایر رنگها» حساب میشه — نه سفید، نه مشکی، نه کرمی.) فرمول همونه:
(0 × 1 × (0 + 0)) + (1 × 1 × (1 − 0)) + 0
سادهسازی میکنیم:
(0 × 1 × 0) + (1 × 1 × 1) + 0 = 0 + 1 + 0 = 1
نتیجهی نهایی ۱ یعنی بله، درسته، این یکی بچهگربه همونیه که باید باهات بیاد خونه. (و اتفاقاً از همهشون نازتر هم بود!)
اون شب، وقتی بچهگربه توی بغلت لم داده و خوابیده، فکری به سرت میزنه: نکنه میتونستی با یه سری کلید برق و یه لامپ، بفهمی که کدوم گربهها با معیارهات جور در میان؟ (آره، یه کم بچهی عجیبی هستی!)
اما خبر نداری که الان دقیقاً داری به یه کشف خیلی مهم نزدیک میشی — کشفی که میتونه جبر منطقی جرج بول رو با مدارهای الکتریکی ترکیب کنه و مسیر ساختن کامپیوترهای دیجیتال رو باز کنه. ولی نترس، قراره قدم به قدم جلو بریم.
برای شروع آزمایشت، یه لامپ و باتری رو مثل همیشه به هم وصل میکنی، اما بهجای یه کلید، دو تا کلید برق میذاری:
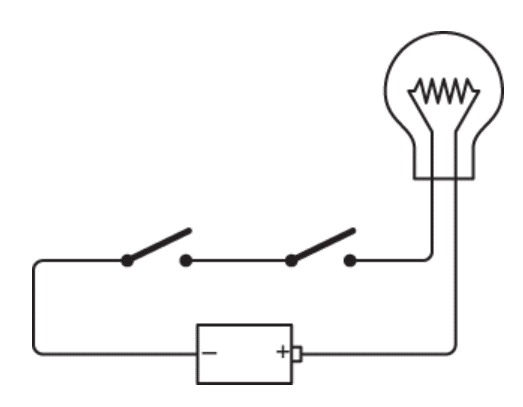
وقتی کلیدها اینطوری پشت سر هم وصل میشن، میگیم به صورت سری (Series) به هم متصل شدن.
حالا اگه فقط کلید سمت چپ رو ببندی، هیچ اتفاقی نمیافته:
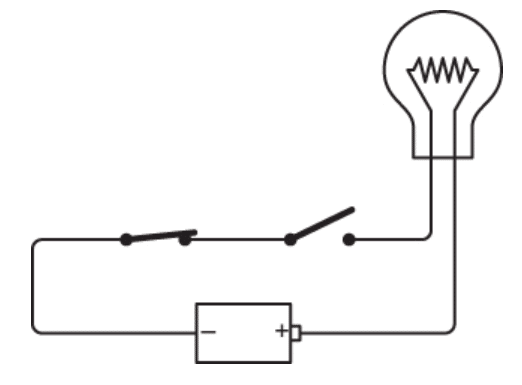
همینطور، اگه کلید سمت چپ باز باشه و فقط کلید سمت راست رو ببندی، باز هم لامپ روشن نمیشه.
لامپ فقط زمانی روشن میشه که هر دو کلید بسته باشن، مثل شکل زیر:
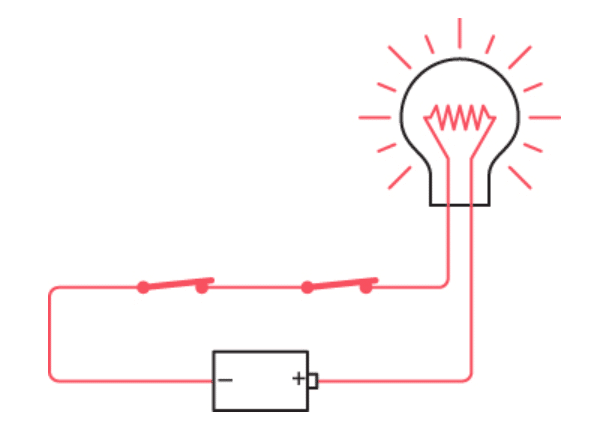
اینجا اون کلمهی کلیدی که باید بهش دقت کنیم «و» (AND) هست. هم کلید سمت چپ و هم کلید سمت راست باید بسته باشن تا جریان برق بتونه از مدار عبور کنه.
در واقع، این مدار داره یه تمرین کوچیک توی منطق انجام میده. به زبون ساده، انگار لامپ داره به این سؤال جواب میده: «آیا هر دو کلید بسته هستن؟»
میتونیم کارکرد این مدار رو با جدول زیر خلاصه کنیم:

اگه کلیدها و لامپ رو بهعنوان عملگرهای بولی در نظر بگیریم، میتونیم بهشون مقدارهای ۰ و ۱ بدیم. صفر یعنی «کلید بازه» و یک یعنی «کلید بستهست». برای لامپ هم صفر یعنی «لامپ خاموشه» و یک یعنی «لامپ روشنه».
حالا فقط کافیه همین جدول رو با این عددها بازنویسی کنیم:

جالبه که اگه جای کلید سمت چپ و سمت راست رو عوض کنیم، نتیجه تغییری نمیکنه. یعنی لازم نیست بدونیم کدوم کلیده کدوم. پس میتونیم جدول رو بهشکلی بنویسیم که خیلی شبیه جدول AND و OR باشه که قبلاً دیدیم:
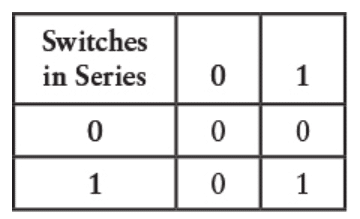
و در واقع، این جدول دقیقاً همون جدول AND ـه. یه بار دیگه نگاه کن:
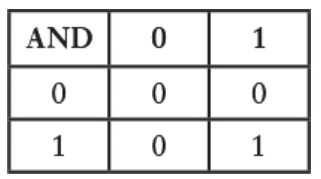
پس این مدار ساده داره یه عملیات AND رو در جبر بولی اجرا میکنه.
حالا بیا دو تا کلید رو یه جور دیگه به هم وصل کنیم…
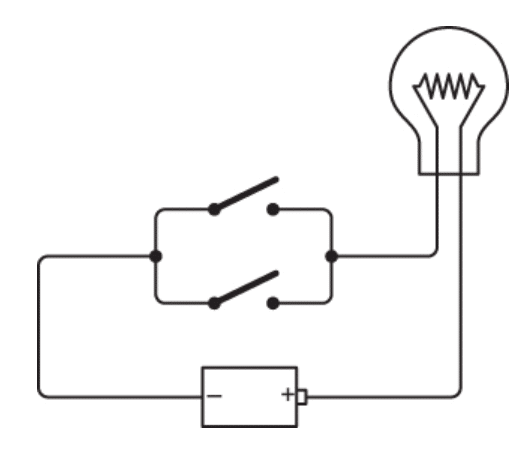
به این نوع اتصال میگن اتصال موازی. فرقش با اتصال قبلی اینه که اینبار لامپ روشن میشه اگه فقط یکی از کلیدها بسته باشه.
مثلاً اگه فقط کلید بالایی رو ببندی، لامپ روشن میشه:
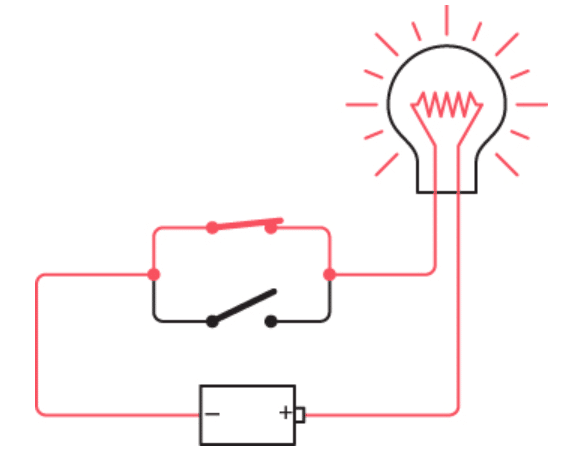
یا اگه فقط کلید پایینی بسته باشه، بازم لامپ روشنه:
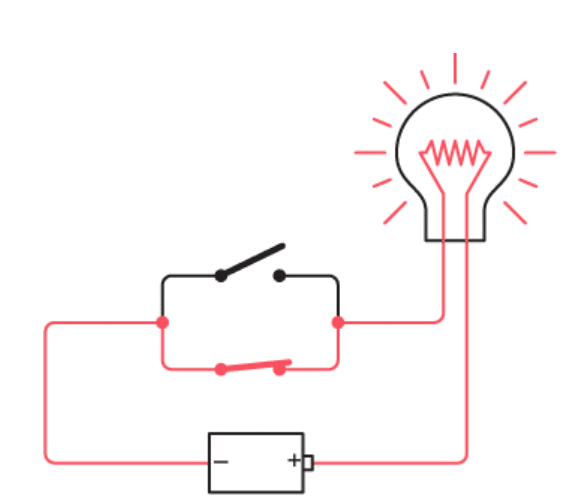
یا حتی اگه هر دو کلید با هم بسته باشن، باز هم لامپ روشنه:
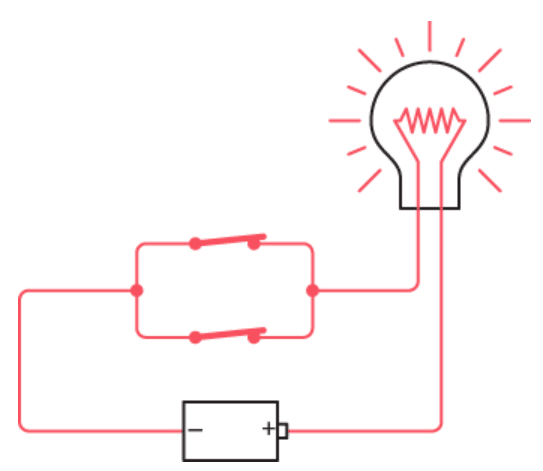
لامپ روشن میشه اگه کلید بالایی یا کلید پایینی بسته باشه. کلمهی کلیدی اینجا «یا» (OR) هست.
دوباره، این مدار داره یه کار منطقی انجام میده. این بار لامپ به این سؤال جواب میده:
«آیا حداقل یکی از کلیدها بستهست؟»
و جدول زیر نشون میده که مدار چطور کار میکنه:

دوباره، اگه از ۰ برای نشون دادن «کلید باز» یا «لامپ خاموش» استفاده کنیم و از ۱ برای «کلید بسته» یا «لامپ روشن»، اون جدول رو میتونیم اینطوری بازنویسی کنیم:

باز هم مهم نیست جای این دو کلید رو عوض کنیم یا نه؛ نتیجه یکسان میمونه. پس جدول رو میتونیم به شکل استانداردِ جدولهای منطقی بازنویسی کنیم:
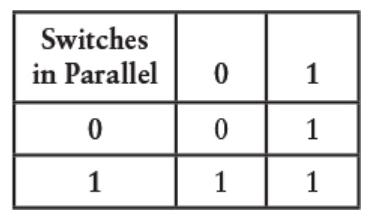
و احتمالاً خودت هم حدس زدی که این دقیقاً همون عملگر OR در جبر بولیه:
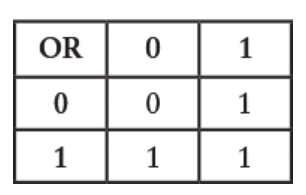
این یعنی دو تا کلیدی که به صورت موازی وصل شدن، در واقع دارن همون کاری رو میکنن که در جبر بولی بهش میگیم OR.
حالا برگردیم به اون موقعی که وارد پتشاپ شدی و گفتی:
«یه گربهی نر، عقیم، که یا سفید باشه یا کرم؛ یا یه گربهی ماده، عقیم، که رنگش فقط سفید نباشه؛ یا هر گربهای که مشکی باشه.»
و فروشنده برای این خواستهی پیچیده، این عبارت بولی رو نوشت:
(M×N×(W+T))+(F×N×(1−W))+B
حالا که فهمیدی دو کلید متصل بهصورت سری یعنی عملگر AND (علامت ×) و دو کلید متصل بهصورت موازی یعنی عملگر OR (علامت +)، میتونی هشت تا کلید رو اینطوری به هم وصل کنی:
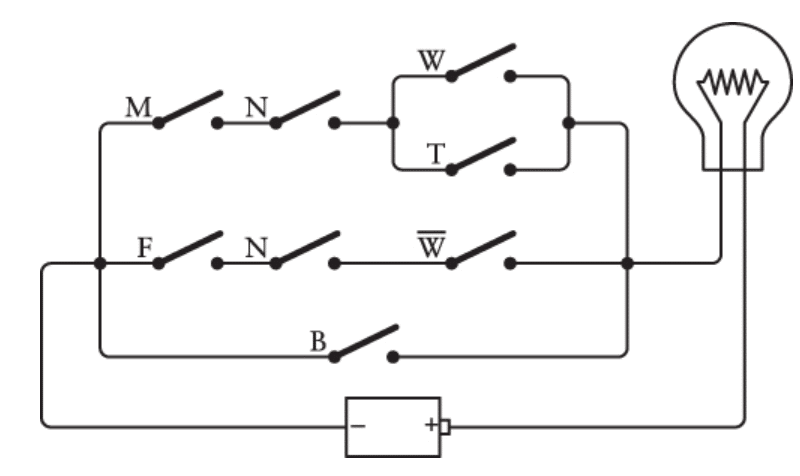
هر کلیدی توی این مدار با یه حرف برچسبخورده — همون حروفی که توی عبارت بولی بودن. حرف W̄ همون NOT W هست، که یه شکل دیگهی نوشتنِ 1 − W محسوب میشه.
در واقع اگه از بالا به پایین و از چپ به راست مدار رو دنبال کنی، ترتیب حروف همون ترتیبیه که توی عبارت بولی میبینی. هر علامت × توی عبارت، دقیقاً همون جاییه که دو کلید (یا گروهی از کلیدها) توی مدار به صورت سری وصل شدن، و هر علامت + جاییه که دو تا بخش از مدار به صورت موازی به هم وصل شدن.
حالا برگردیم به همون اولین گربهای که فروشنده آورد: یه گربهی نر، کرم، ولی عقیم نبود. حالا کلیدهای مربوطه رو ببند…
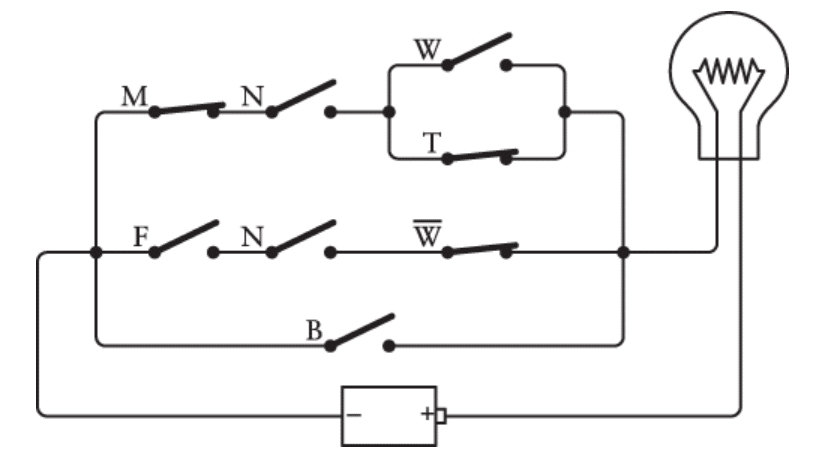
با اینکه کلیدهای M، T و NOT W بسته بودن، هنوز مدار کامل نمیشه که لامپ روشن بشه. بعدش فروشنده یه گربهی مادهی سفید و عقیم آورد:
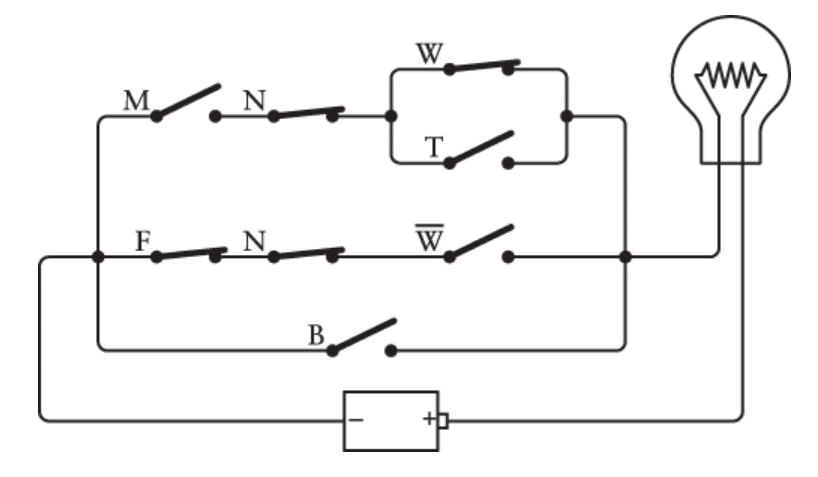
اما این بار هم، باز همون مشکل پابرجاست — کلیدهای درست بسته نشدن که مدار رو کامل کنن.
اما بالاخره، فروشنده یه گربهی مادهی خاکستری و عقیم آورد:
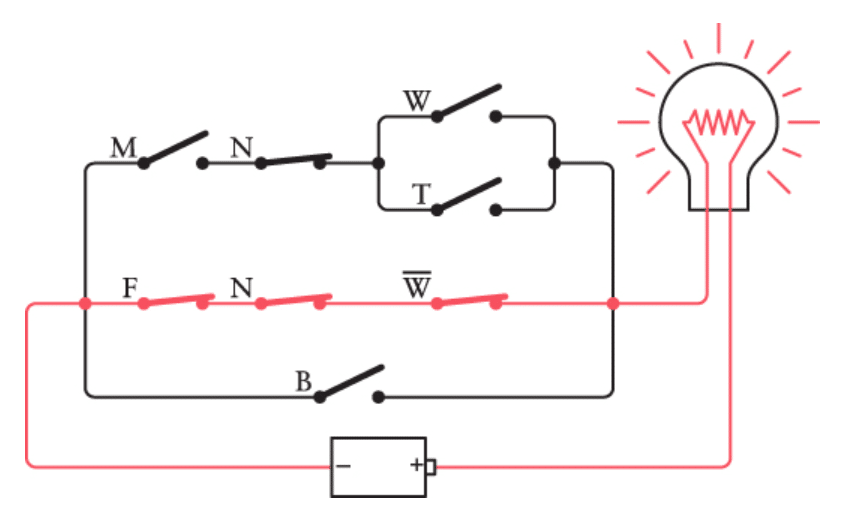
و این یکی دقیقاً همون چیزی بود که نیاز بود — مدار کامل شد، لامپ روشن شد، و یعنی این بچهگربه با همهی شرایطت جور در میاومد.
جرج بول هیچوقت همچین مداری رو با سیم و کلید و لامپ نبست. هیچوقت لذت دیدنِ یه عبارت بولی که با سختافزار واقعی روشن و خاموش میشه رو تجربه نکرد. البته یکی از موانعش این بود که لامپ رشتهای ۱۵ سال بعد از مرگ بول اختراع شد. ولی جالبه بدونی که تلگراف ۱۰ سال قبل از انتشار کتاب «قوانین اندیشه»ی بول اختراع شده بود — و یه بخش مهم از سیستم تلگراف، یه وسیلهی ساده بود که میتونست عملیات منطقی رو خیلی سریعتر و دقیقتر از کلیدهای معمولی انجام بده.

