کد مورس حدود سال ۱۸۳۷ توسط ساموئل فینلی بریس مورس (۱۷۹۱–۱۸۷۲) اختراع شد، که بعداً تو این کتاب بیشتر باهاش آشنا میشیم. این کد بعداً توسط افراد دیگهای، بهخصوص آلفرد ویل (۱۸۰۷–۱۸۵۹)، توسعه پیدا کرد و به چند نسخهی مختلف تبدیل شد. سیستمی که تو این کتاب توضیح داده شده، بهطور رسمی به اسم کد مورس بینالمللی شناخته میشه.
اختراع کد مورس با اختراع تلگراف گره خورده، که بعداً تو این کتاب بیشتر دربارهش حرف میزنیم. همونطور که کد مورس یه مقدمهی خوب برای شناخت ماهیت کدهاست، تلگراف هم سختافزاری داره که میتونه کارکرد یه کامپیوتر رو تقلید کنه.
بیشتر آدما میگن فرستادن کد مورس راحتتر از دریافت کردنشه. حتی اگه کد مورس رو از حفظ بلد نباشی، میتونی بهراحتی از جدولی که تو فصل قبل دیدی استفاده کنی، که به ترتیب الفبا مرتب شده:
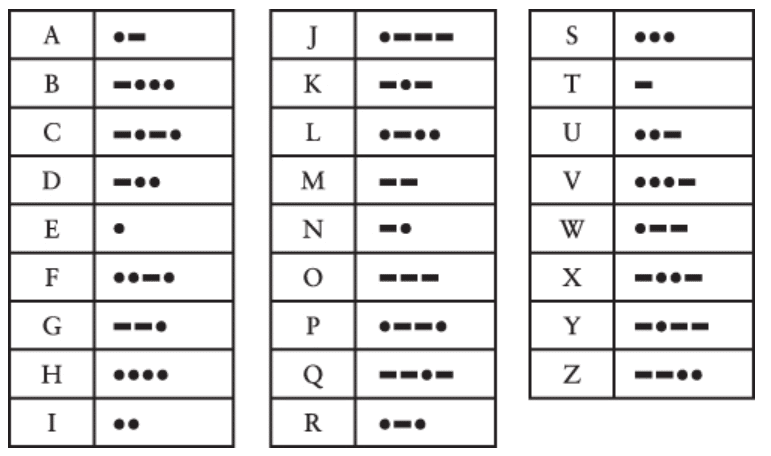
دریافت کد مورس و برگردوندنش به کلمات خیلی سختتر و زمانبرتر از فرستادنه، چون باید برعکس عمل کنی تا بفهمی کدوم حرف به یه توالی خاص از نقطهها و خطها ربط داره. اگه کدها رو از حفظ بلد نباشی و مثلاً یه خط-نقطه-خط-خط دریافت کنی، باید کل جدول رو حرف به حرف نگاه کنی تا بالاخره بفهمی این حرف Yـه.
مشکل اینجاست که ما یه جدول داریم که این تبدیل رو نشون میده:
حرف الفبا → نقطهها و خطهای کد مورس
ولی جدولی نداریم که بتونه برعکس عمل کنه:
نقطهها و خطهای کد مورس → حرف الفبا
تو مراحل اولیهی یادگیری کد مورس، داشتن همچین جدولی مطمئناً خیلی بهدردبخور میبود. ولی اصلاً مشخص نیست چطور میتونیم همچین جدولی درست کنیم. تو نقطهها و خطها چیزی نیست که بتونیم به ترتیب الفبا مرتبش کنیم.
خب، پس بیخیال ترتیب الفبا بشیم. شاید یه راه بهتر برای مرتب کردن کدها این باشه که اونا رو بر اساس تعداد نقطهها و خطهاشون گروهبندی کنیم. مثلاً یه توالی کد مورس که فقط یه نقطه یا یه خط داره، فقط میتونه دو تا حرف رو نشون بده، که E و T هستن:
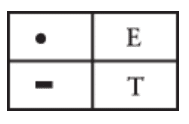
یه ترکیب از دقیقاً دو تا نقطه یا خط، چهار تا حرف دیگه رو میده: I، A، N و M:
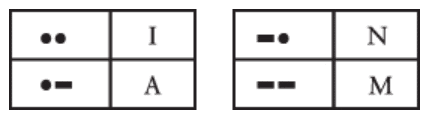
یه الگوی سهتایی از نقطهها یا خطها، هشت تا حرف دیگه بهمون میده:
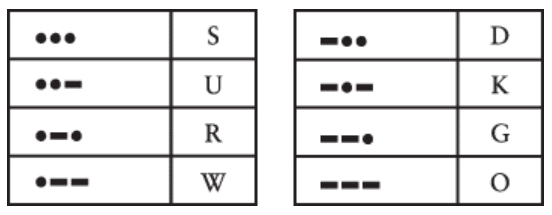
و بالاخره (اگه بخوایم این تمرین رو قبل از پرداختن به اعداد و علامتهای نگارشی تموم کنیم)، توالیهای چهار تایی از نقطهها و خطها، ۱۶ تا حرف دیگه رو بهمون میدن:
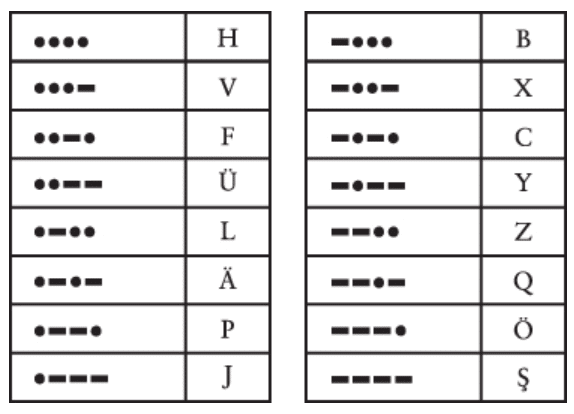
این چهار تا جدول با هم ۲ + ۴ + ۸ + ۱۶ تا کد برای ۳۰ حرف میدن، که ۴ تا بیشتر از ۲۶ حرف الفبای لاتینه. به همین دلیل، میبینی که ۴ تا از کدها تو جدول آخر برای حروف دارای علامتن: سه تا با اوملوت (¨) و یکی با سدی (¸).
این چهار جدول قطعاً میتونن وقتی کسی داره برات کد مورس میفرسته کمک کنن. وقتی کد یه حرف خاص رو دریافت میکنی، میدونی چند تا نقطه و خط داره و دستکم میتونی بری سراغ جدول درست و پیداش کنی. هر جدول بهصورت منظم مرتب شده، از کد تمامنقطه تو گوشهی بالا سمت چپ شروع میشه و به کد تمامخط تو گوشهی پایین سمت راست ختم میشه.
میتونی الگویی تو اندازهی این چهار جدول ببینی؟ هر جدول دو برابر جدول قبلی کد داره. این منطقیه: هر جدول شامل همهی کدهای جدول قبلی به علاوهی یه نقطهست، و همهی کدهای جدول قبلی به علاوهی یه خط.
میتونیم این روند جالب رو اینجوری خلاصه کنیم:
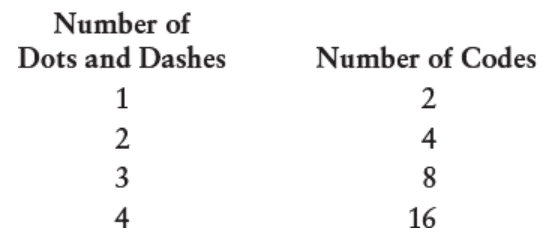
هر کدوم از این چهار جدول دو برابر جدول قبلی کد داره. پس اگه جدول اول ۲ تا کد داشته باشه، جدول دوم ۲ × ۲ تا کد داره، و جدول سوم ۲ × ۲ × ۲ تا کد. یه راه دیگه برای نشون دادنش اینه:
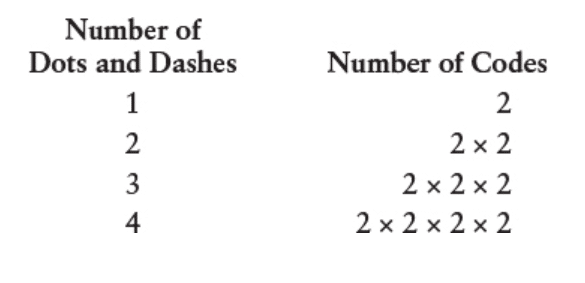
وقتی با یه عدد روبهرو هستیم که تو خودش ضرب میشه، میتونیم از توانها برای نشون دادنش استفاده کنیم. مثلاً ۲ × ۲ × ۲ × ۲ رو میشه به صورت ۲ به توان ۴ (۲^۴) نوشت. اعداد ۲، ۴، ۸ و ۱۶ همشون توانهای ۲ هستن، چون میتونی با ضرب کردن ۲ تو خودش بهشون برسی. این خلاصه رو میشه اینجوری هم نشون داد:
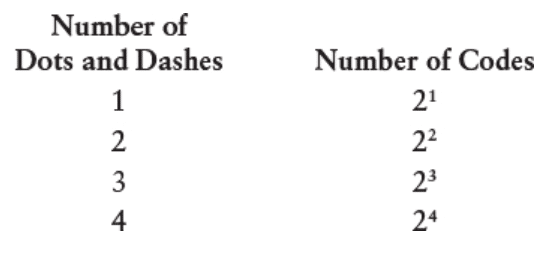
این جدول خیلی ساده شده. تعداد کدها خیلی راحت، ۲ به توان تعداد نقطهها و خطفاصلههاست:
تعداد کدها = ۲تعداد نقطهها و خطفاصلهها
توانهای ۲ توی کدها، و مخصوصاً توی این کتاب، خیلی زیاد پیدا میشن. یه مثال دیگهش رو توی فصل بعدی میبینی.
برای اینکه رمزگشایی کد مورس حتی آسونتر هم بشه، شاید بخوای چیزی شبیه این نمودار درختی بزرگی که اینجا نشون داده شده رو بکشی.
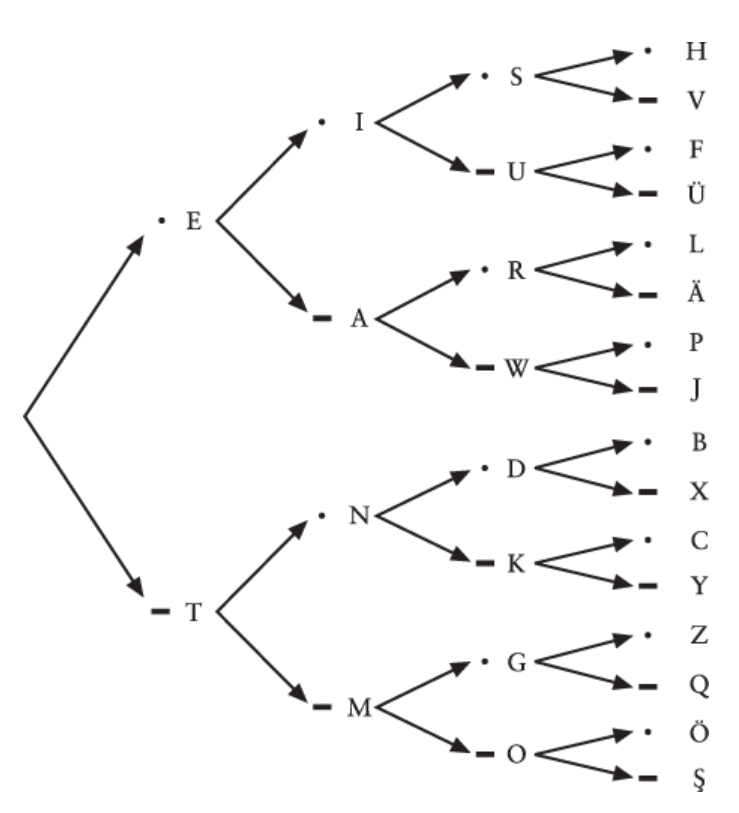
این نمودار حرفهایی رو نشون میده که از هر دنبالهی متوالی خاصی از نقطهها و خطفاصلهها به دست میآن. برای رمزگشایی یه دنبالهی خاص، فلشها رو از چپ به راست دنبال کن. مثلاً فرض کن میخوای بدونی چه حرفی متناظر با کد نقطه-خط-نقطه هست. از سمت چپ شروع کن و نقطه رو انتخاب کن؛ بعد همینطور از طریق فلشها به سمت راست حرکت کن و خط رو انتخاب کن و بعد یه نقطهی دیگه. حرف R هست که کنار سومین نقطه نشون داده شده.
اگه بهش فکر کنی، ساختن همچین جدولی احتمالاً از اول برای تعریف کد مورس ضروری بوده. اولاً، این تضمین میکنه که اشتباه احمقانهی استفاده از یک کد برای دو حرف مختلف رو مرتکب نمیشی! ثانیاً، مطمئن میشی که از تمام کدهای ممکن استفاده میکنی بدون اینکه دنبالههای نقطهها و خطفاصلهها رو بیدلیل طولانی کنی.
با این ریسک که این جدول رو فراتر از محدودیتهای صفحهی چاپی گسترش بدیم، میتونستیم اون رو برای کدهای پنج نقطه و خطفاصله ادامه بدیم. یه دنباله دقیقاً پنج نقطه و خطفاصله، ۳۲ (۲ × ۲ × ۲ × ۲ × ۲، یا ۲۵) کد اضافی به ما میده. معمولاً این برای ده عدد و ۱۶ نماد نقطهگذاری تعریف شده توی کد مورس کافیه، و در واقع، اعداد با پنج نقطه و خطفاصله کدگذاری میشن. اما خیلی از کدهای دیگهای که از دنبالهای از پنج نقطه و خطفاصله استفاده میکنن، به جای علائم نقطهگذاری، حروف لهجهدار رو نشون میدن.
برای اینکه تمام علائم نقطهگذاری رو هم شامل بشه، سیستم باید به شش نقطه و خطفاصله گسترش پیدا کنه، که ۶۴ (۲ × ۲ × ۲ × ۲ × ۲ × ۲، یا ۲۶) کد اضافی به ما میده برای مجموعاً ۲ + ۴ + ۸ + ۱۶ + ۳۲ + ۶۴، یا ۱۲۶ کاراکتر. این برای کد مورس زیادهرویه، که خیلی از این کدهای طولانیتر رو تعریفنشده میذاره، که در این مفهوم به کدی اشاره داره که معنی خاصی نداره. اگه داشتی کد مورس دریافت میکردی و یه کد تعریفنشده میگرفتی، میتونستی تقریباً مطمئن باشی که یه نفر اشتباه کرده.
چون ما به اندازه کافی باهوش بودیم که این فرمول کوچیک رو بسازیم،
تعداد کدها = ۲تعداد نقطهها و خطفاصلهها
میتونستیم ادامه بدیم و بفهمیم که با استفاده از دنبالههای طولانیتر چند تا کد به دست میآریم:
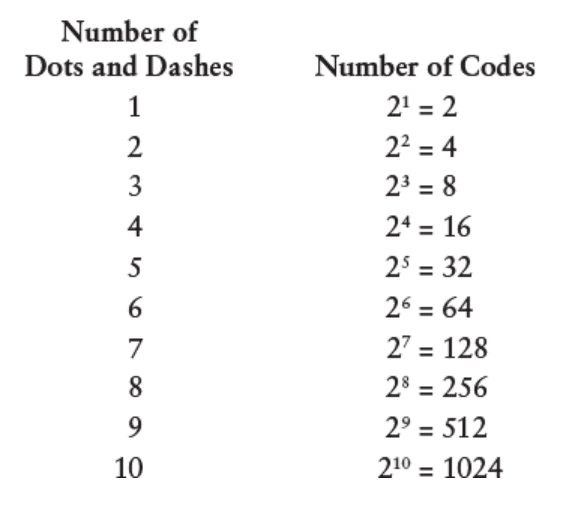
خوشبختانه، لازم نیست واقعاً همهی کدهای ممکن رو بنویسیم تا بفهمیم چند تا کد خواهیم داشت. تنها کاری که باید بکنیم اینه که عدد ۲ رو بارها و بارها در خودش ضرب کنیم.
کد مورس رو باینری (که به معنای واقعی کلمه «دو به دو» هست) میگن چون اجزای تشکیلدهندهی کد فقط از دو چیز تشکیل شده – نقطه و خط فاصله. این شبیه یه سکهست که فقط میتونه روی شیر یا خط بیفته. سکههایی که ده بار پرتاب میشن میتونن ۱۰۲۴ دنبالهی مختلف از شیر و خط داشته باشن.
ترکیباتی از اشیای باینری (مثل سکهها) و کدهای باینری (مثل کد مورس) همیشه با توانهای دو توصیف میشن. عدد دو تو این کتاب خیلی مهمه.

